[toc]

期权的价值特征

期权价值变化特征

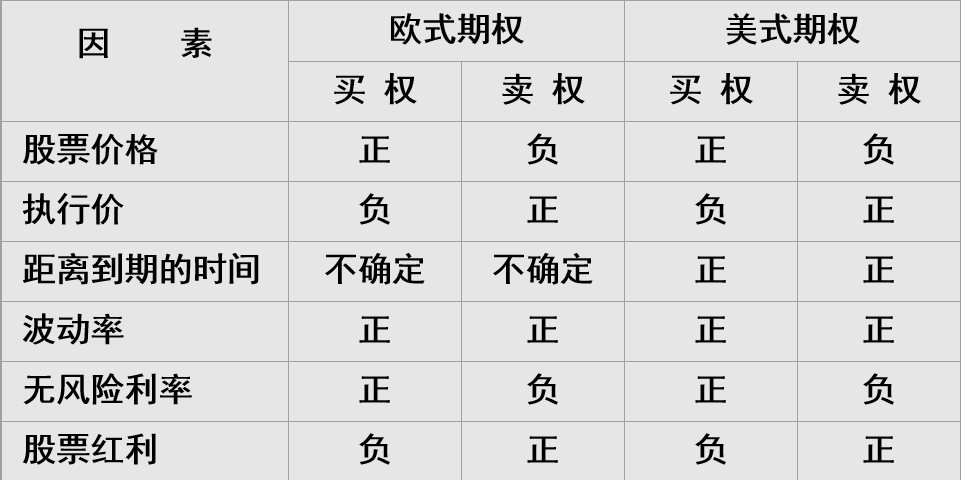
直观解释

股票价格和执行价；距离到期的时间
红利：在除息日，红利将减少股票的价格
波动率：用来度量股票未来价格不确定变化程度的指标。随着波动率增加，期权的价值也会增加，即波动率增加对期权的影响总是有利的。
无风险利率：无风险利率对期权价值的影响是比较复杂的。影响来自两个方面，一方面，股票价格的预期增长率随着利率的上升而上升；另一方面，利率上升将提高贴现率，减少了期权多头收到的未来现金流的现值。对于卖权来说，这两种作用都是不利的，因此，利率越高，卖权的价值越低。对于买权来说，前一种作用是有利的，后一种作用是不利的。可以证明，前一种作用相对于后一种作用占优，因此，利率越高，买权的价值越高。

期权价值结构

实值期权、平价期权、虚值期权

对于看涨期权来说，为了区别标的资产市价（S）与协议价格（X）的关系如下：

$S > X$ 时的看涨期权称为实值看涨期权（In the Money），如果期权立即执行，将具有正收益特征；
$S = X$ 时的看涨期权称为平价（两平）看涨期权（At the Money），如果期权立即执行，将具有零收益特征；
$S < X $时的看涨期权称为虚值看涨期权（Out of the Money）。

对于看跌期权来说，类似可以定义其状态。

其中：深度实值看涨期权：$S \gg X$；深度虚值看涨期权：$S \ll X$

期权的内在价值

期权的内在价值（Intrinsic Value）：期权多头行使期权时可以获得的收益，一般只有美式期权可以马上看到。其中：

美式看涨期权的内在价值为 $\max(S - X,0)$，美式看跌期权的内在价值为 $\max(X - S,0)$

内在价值原理：期权的价格决不会低于其内在价值，即 $c > \max(S - X,0) \geq S -X$（以看涨期权为例）

欧式期权的内在价值

欧式看涨期权在到期日 T 时刻的内在价值为 \[ \max(S_{T} - X,0) \]

无收益资产的欧式看涨期权在 t 时刻的内在价值为： \[ \max(S_{t} - Xe^{- r(T - t)},0) \]

有收益资产欧式看涨期权在 t 时刻的内在价值为 \[ \max(S_{t} - D - Xe^{- r(T - t)},0) \]

其中D为标的资产在期权持有期内红利收益现金流在 t 时刻的现值。

无收益资产欧式看跌期权在 t 时刻的内在价值为 \[ X{\ e}^{- r(T - t)} - S \]

有收益资产欧式看跌期权在 t 时刻的内在价值为 \[ Xe^{- r(T - t)} + D - S\ \]

当然，当标的资产市价高于协议价格时，期权多方是不会行使期权的，因此欧式看跌期权的内在价值应 $\geq 0$

期权的时间价值

期权的时间价值（Time Value）：期权价格与其内在价值之间的差额，或称投机价值。其中：

期权的时间价值反映了交易商愿意为标的资产价格波动的不确定性所支付的代价。
标的资产价格的波动率越高，期权的时间价值就越大。
时间价值随着到期期间的增长而增加。

当股价接近执行价格时，不确定性是最大的，时间价值最高。而对于深度实值看涨期权与深度虚值看涨期权来说，相应的其时间价值极低。

欧式期权的时间价值

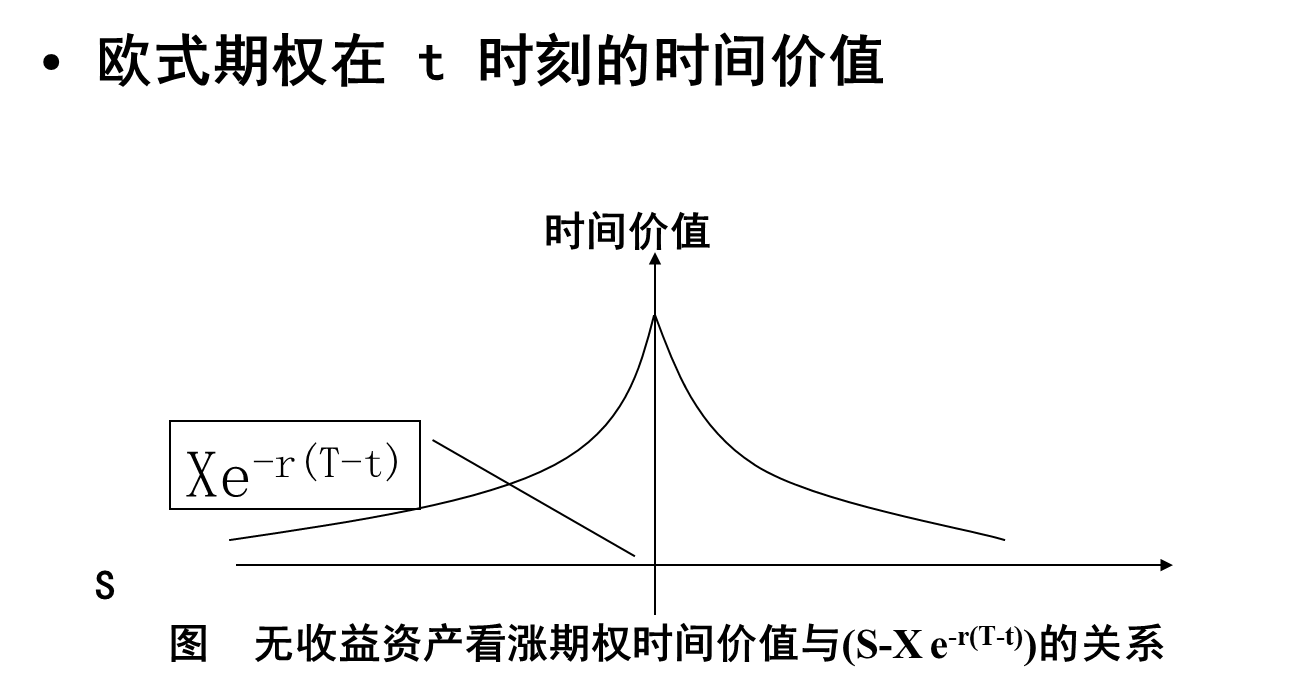
RT，以无收益资产看涨期权为例，当$S = X e^{- r(T - t)}$时，期权的时间价值最大。

同样的：

有收益资产看涨期权的时间价值在$S = D + \ Xe^{- r(T - t)\ }$点最大，
无收益资产欧式看跌期权的时间价值在$S = Xe^{- r(T - t)}$点最大，
有收益资产欧式看跌期权的时间价值在$S = Xe^{-r(T - t)}+ D$点最大,
无收益资产美式看跌期权的时间价值在$S = X$点最大，
有收益资产美式看跌期权的时间价值在$S = \ X+D$ 点最大。

Call-Put Parity

Non-Dividend, European Call Option v.s. European Put Option

Non-Dividend European Option 平价关系 \[ c + Xe^{- r(T - t)} = p + S_0 \]

其中 c 为 call option fee , X 为交割价格， r 为无风险利率， T-t 为时间间隔， p 为 put option fee , $S_0$ 为一单位标的资产的价格

证明过程：

复制的思想：考虑以下两个投资组合

产品A：一份 European Call Option + 金额为 $Xe^{-r(T-t)}$ 的债券 or 无风险投资

产品B：一份有效期与协议价格均与上述期权相同的 European Put Option + 一单位标的资产

期权到期时，两份资产价值均为 $\max (S_T,X)$ ，European Option 在执行日之前不能提前执行，故两个产品组合必须在 t 时刻具有相同的价值，否则存在套利机会。

反证法

Dividend, European Call Option v.s. European Put Option

Dividend European Option 平价关系 \[ c + D + Xe^{- r(T - t)} = p + S \]

证明：在标的资产有收益的情况下，我们只要把前面的组合 A 中的现金改为 $D + Xe^{- r(T-t)}$ 即可。

Non-Dividend, American Call Option v.s. American Put Option

Non-Dividend American Option 平价关系： \[ S - X < C - P \leq S - Xe^{- r(T - t)} \]

证明：

不等式右端：$P > p$ 且 $c = C$

不等式左端：

复制：考虑以下两个组合，在这两个组合中，期权的执行价格和到期日相同：

组合 A ：一份 European Call Option + 金额为 X 的现金

组合 B ：一份 American Put Option + 一单位标的资产

考虑 American Option 没有提前执行、提前执行情况：

没有提前执行：

组合 A ：$\max(S_T,X)+Xe^{r(T-t)}-X$

组合 B ：$\max(S_T,X)$

在 $\tau$ 时刻提前执行：

组合 A ：$>Xe^{r(\tau -t)}$

组合 B ：$X$

故组合 A 的价值大于组合 B

反证法

Dividend, American Call Option v.s. American Put Option

Dividend American Option 平价关系： \[ S - D - X\ < \ C - P\ < \ S - Xe^{- r(T - t)} \]

证明：只需要把组合 A 的现金改为 $D + X$ 即可。

上述内容参考书籍：

《数量金融》（Paul Wilmott）Chapter 2

《The Mathematics of Finance: Modeling and Hedging》Chapter 1 1.2.1&1.3

期权价格的上下限

如下约定，小写字母为 European Options，大写字母为 American Options

Call Options：

对于 American Call Option 和 European Call Option，标的资产价格就是 Call Option 价格的上限： \[ \displaylines{c \leq S_0 \\ C \leq S_0} \]

其中 $S_0$ 代表标的资产价格。反之，套利策略：购买股票，出售期权。（理解：否则没必要买期权）

对于 Non-Dividend Stock の European Call Option，其下限： \[ c \geq \max(S_0 - Xe^{- r(T - t)},0) \]

证明：

考虑如下两个组合：

组合A：一份 European Call Option 加上金额为 $Xe^{- r(T - t)}$ 的现金 or 无风险投资

组合B：一单位标的资产

且期权的价值一定为正，可推得 \[ \max(S_T,X) \geq S_T \Rightarrow c+Xe^{-r(T-t)} \geq S_0 \Rightarrow c \geq \max(S_0-Xe^{-r(T-t)},0) \]

对于 Non-Dividend Stock の American Call Option 来说，其价格的下限： \[ C \geq \max\lbrack S - Xe^{- r(T - t)},0\rbrack \]

证明：由于 $C \geq c$（在到期之前，行使无红利股票的 Call Option 永远不是最佳选择， American Options 的持有者行使期权的机会包括 European Options 行使期权的机会，故 $V_{American} \geq V_{European}$ ）

对于 Dividend Stock の European Call Option，其价格的下限： \[ c \geq \max(S - D - Xe^{- r(T - t)},0) \]

证明：只要将上述组合 A 的现金改为 $D + Xe^{- r(T - t)}$ 即可，其中 D 为期权有效期内资产收益的 t 时刻现值。

当股息在预计之中时，我们将不再有 American Call Option 是否提前行使的结论。有时在除息之前，行使 American Call Option 为最优，但在其他时刻行使 American Call Option 不会是最优策略。

Put Options：

对于 American Put Option，其价格的上限为： \[ P \leq X \]

而对于 European Put Option，其价格的上限为： \[ p \leq Xe^{- r(T - t)} \]

其中 X 为交割价格。反之，套利策略：卖出一单位期权，同时将卖出期权的所得费用以无风险利率进行投资。

对于 Non-Dividend Stock の European Put Option，其价格的下限： \[ p \geq \max(Xe^{- r(T - t)} - S,0) \]

证明：

考虑以下两种组合：

组合C：一份 European Put Option 加上一单位标的资产

组合D：金额为 $Xe^{- r(T - t)}$ 的现金

且期权价值一定为正，仿照上方可推得 \[ \max(S_T,X) \geq X \Rightarrow p+S_0 \geq Xe^{-r(T-t)} \Rightarrow p \geq \max(Xe^{-r(T-t)}-S_0,0) \]

对于 Dividend Stock の European Put Option ，其价格的下限： \[ p \geq \max(D + Xe^{- r(T - t)} - S,0) \]

证明：只要将上述组合 D 的现金改为$D + Xe^{- r(T - t)}$即可。

从以上分析可以看出，European Option 的下限实际上就是其内在价值。

对于 Non-Dividend Stock の American Put Option 来说，其价格的下限： \[ P \geq \max(K - S_{0},0) \]

考虑：由于 American Put Option 不需要折现，可以提前行权，故其价格下限相对于 European Put Option ，可选择在 0 时刻交割。

提前执行 American Option 是否合理？

Non-Dividend Stock American Call Option

提前执行 Non-Dividend Stock の American Call Option 是不明智的，即同一种无收益标的资产的 American Call Option 和 European Call Option 的价值是相同的，即 $C = c$ 。

推导：$C \geq c \geq \max\lbrack S - Xe^{- r(T - t)},0\rbrack > S - X$ ，最优的策略是要么持有 American Call Option ，要么出售进行交易。而放弃提前执行的权力。

直观理解：

现金会产生效益，提前执行 American Call Option 得到的标的资产无收益，且 American Call Option 的时间价值总为正。

T 时刻的 pay-off 为 $S_T-K$ ，折现到 t 时刻为 $S_t-Ke^{-r(T-t)} > S_t-K$ 没有必要提前执行权利。

Non-Dividend Stock American Put Option

最简单的情况：资产几乎没有价值，此时执行 American Put Option 。

是否提前执行 Non-Dividend Stock の American Put Option ，主要取决于期权的实内在价值额 $(X-S_0)$ 、无风险利率水平等因素。一般而言，只有 $(X-S_0)$较大，或者无风险利率较大时，才会提前执行 American Put Option 是有利的。

Dividend Stock American Option

在有收益情况下，由于提前执行 Dividend Stock American Option 可较早获得标的资产，从而获得现金收益及其派生的利息，故只有在除权前的瞬时时刻提前执行 Dividend Stock の American Call Option 才有可能是最优的。

考察在最后一个除权日 $t_n$ 提前执行的条件。若在 $t_n$ 时刻提前执行期权，则期权多方获得 $S_n-X$ 的收益。若不提前执行，则标的资产价格由于除权将降到 $S_n-D_n$ 。此时，在 $t_n$ 时刻的期权价值 \[ C_n \geq c_n \geq \max(S_n-D_n-Xe^{-r(T-t_n)},0) \] 此时，

若 $S_n-D_n-Xe^{-r(T-t_n)} \geq S_n-X$ ，即 $D_n \leq X[1-e^{-r(T-t_n)}]$ ，则在 $t_n$ 时刻执行 American Call Option 是不明智的。
若 $S_n-D_n-Xe^{-r(T-t_n)} \leq S_n-X$ ，即 $D_n \geq X[1-e^{-r(T-t_n)}]$ ，则在 $t_n$ 时刻执行 American Call Option 是明智的。

而这实际上只有当 $t_n$ 时刻标的资产价格足够大时才是合理的。

对于任意在 $t_{i}$ 时刻不能提前执行 Dividend Stock の American Call Option 充分条件是： \[ D_{i} \leq X\lbrack 1 - e^{- r(t_{i + 1} - t_{i})}\rbrack \]

Dividend Stock の American Put Option 不能提前执行的充分条件是： \[ \displaylines{D_{i} \geq X\lbrack 1 - e^{- r({t_{i}}_{+ 1} - t_{i})}\rbrack \\ D_{n} \geq X\lbrack 1 - e^{- r(T - t_{n})}\rbrack} \]

提前执行期权的权利价值正是 American Option 和 European Option 的区别所在，只有股票附有红利时，该权利才会凸显价值。

Financial Derivatives Chapter 4：Options Pricing Principles